| Mathe | Physik | Online-HÜs | Lehrer | Kontakt |
 |
 |
 |
| Klassenstufe 8 - Terme und Gleichungen | ||
 |
 |
Vereinfachen von einfachen Termen (ohne Binomische Formeln) |
|
|
Termumformungen und Binomische Formeln |
|
 |
Binomische Formeln |
|
 |
Fiktives Gespräch von Tim und Tom über Terme |
 |
 |
Terme vereinfachen
(Produkte,Summen,Klammerregeln) (Nur in der Excelversion: zufallsgenerierte Klapptests und somit immer wieder neue Aufgaben) |
|
|
Terme vereinfachen und
Gleichungen lösen (Nur in der Excelversion: zufallsgenerierte Klapptests und somit immer wieder neue Aufgaben) |
|
|
Terme vereinfachen
(verschiedene Rechenregeln) (Nur in der Excelversion: zufallsgenerierte Klapptests und somit immer wieder neue Aufgaben) |
|
|
Terme vereinfachen,
Faktoren ausklammern, Gleichungen aufstellen, Gleichungen
lösen (Nur in der Excelversion: zufallsgenerierte Klapptests und somit immer wieder neue Aufgaben) |
|
|
Bruchgleichungen
lösen (Nur in der Excelversion: zufallsgenerierte Klapptests und somit immer wieder neue Aufgaben) |
| Klassenstufe 8 - Terme und Gleichungen |
| Terme und Variablen |
| Wie sieht der
perfekte Tag eines Mathematikers
aus? Morgens TERME,
abends THERME.
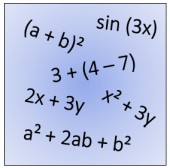  Terme sind Rechenausdrücke aus Zahlen, Rechenzeichen und sogar Buchstaben. Zahlen und Rechenzeichen solltest du mittlerweile kennen. Bei den Buchstaben spricht man von Variablen. Eine Variable ist wie ein schön verpacktes Geschenk. Es steht vor dir auf dem Tisch und es könnte alles Mögliche drin sein: vielleicht ein Ball, ein Computerspiel oder ein spannendes Buch. Aber nicht enttäuscht sein: In den Variablen-Geschenken sind nur Zahlen drin. Da wir aber vor dem Auspacken nicht wissen, welche Zahl drin ist, steht die Variable als Platzhalter für alle Zahlen. Wenn in deinem Term, also deinem Rechenausdruck zweimal ein "x" vorkommt, weißt du zwar noch nicht, für welche Zahl die Variable steht, aber du kannst sicher sein, dass es jedesmal dieselbe Zahl ist. Wenn ein "x" und ein "y" vorkommen, können die beiden unterschiedlichen Variablen für verschiedene Zahlen stehen. Es können aber auch zufällig die gleichen Zahlen sein. |
| Kommuntativgesetz |
Jetzt stellen wir uns
mal ein paar Variablen auf dem Tisch
vor. Die können wir natürlich beliebig auf dem Tisch vertauschen. Es bleiben immer vier blaue und drei weiße Geschenke bzw. Variablen. Die Reihenfolge in einer Summe (4 blau + 3 weiß) kann vertauscht werden (3 weiß + 4 blau).  Die Erlaubnis zum Vertauschen hält man im Vertauschungsgesetz fest. Man nennt es auch Kommutativgesetz. Der Name kommt übrigens vom lateinischen „commutare“ für „vertauschen“. Das gilt aber nicht nur für Summen. Auch für Produkte gilt das Kommutativgesetz. Es ist ja egal, ob man 5 mal 2 Euro oder 2 mal 5 Euro bekommt.  Beide Kommutativgesetze gelten natürlich nicht nur für Zahlen, sondern auch für Variablen. |
| Kommutativgesetz Bei einer Summe kann man beliebig Summanden vertauschen. Allgemein schreibt man für beliebige Zahlen a und b: a + b = b + a Beispiel: 12 + 6 = 6 + 12 = 18 Bei einem Produkt kann man beliebig Faktoren vertauschen. Allgemein schreibt man für beliebige Zahlen a und b: a · b = b · a Beispiel: 12 · 6 = 6 · 12 = 72 |
| Potenzen |
| Als Variablen kann
neben
einem normalen x auch mal ein x² vorkommen. Was kann man sich
darunter vorstellen? Gehen wir erst mal einen Schritt zurück. Mathematiker sind ein wenig faul und daher versucht man die Addition 2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2 = kürzer zu schreiben. Das ist natürlich kein Problem. Das sind 25 Zweier. Und man schreibt kürzer 25 · 2. 2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2 = 25 · 2 = 50 Du kannst aus einer langen Addition gleicher Zahlen einfach eine kurze Multiplikation machen und einiges an Schreibarbeit ersparen. Das funktioniert sogar mit Variablen. Berechnen kann man den Term zwar nicht, aber zusammenfassen und kürzer schreiben. x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x+x = 25 · x Geht das mit dem Zusammenfassen einer Multiplikation auch? Schaut man sich das Produkt 2·2·2·2·2·2·2·2·2·2 = an, so kann man 10 mal abwechselnd „2“ und „mal“ im Taschenrechner eingeben. Du kannst aber auch hier aus einer langen Multiplikation gleicher Zahlen einfach eine kurze Potenz machen. Die Mathematiker haben sich dazu eine kürzere Schreibweise ausgedacht. 2·2·2·2·2·2·2·2·2·2 = 210 Mit Variablen geht es auch. Auch hier kann man den Wert wieder nicht berechnen, aber kürzer schreiben. x·x·x·x·x·x·x·x·x·x = x10 So man kann direkt schon eine erste Rechenregel für die Vereinfachung von Termen formulieren. |
| Gleiche
Faktoren
zusammenfassen Bei Produkten, also Multiplikationsaufgaben, kann man gleiche Faktoren zu Potenzen zusammenfassen. Beispiele: x·x·x = x3 x·x·x·x·y·y = x4 · y2 Um später besser zu sehen, welche Summanden sich zusammenfassen lassen, sortiert man die Variablen in einem Produkt alphabetisch. |
| Summanden zusammenfassen |
| Gleiche Faktoren kann
man
zu Potenzen zusammenfassen, aber bei den Aufgaben
im Mathebuch kommen natürlich Plus, Minus und Mal
gemischt vor. Bei verschiedenen Rechenzeichen
muss man ganz genau aufpassen, in welcher Reihenfolge man
vorgehen muss und was man zusammenfassen darf. Die Reihenfolge "Punkt vor Strich!" aus der Grundschule kann man dabei noch etwas erweitern. Plus und Minus sind weiterhin Looser und kommen als Letztes. Mal und Geteilt sind cooler, aber es geht noch wichtiger. Als erstes muss man sich die Klammern vornehmen und danach kommen die Potenzen. Nimmt man die Anfangssilben von "Klammer, Potenz, Punkt, Strich" zu einem Wort zusammen erhält man KLA-PO-PU-STRI. Das hört sich nach einem lustigen Wesen an. Ist es auch. Betrachte das folgende Klapopustri und du wirst die Reihenfolge nie mehr vergessen.  Hat man alle Klammern, Potenzen und Multiplikationsaufgaben vereinfacht, so ist es wichtig, dass man weiß, was man am Ende zusammenfassen darf. Wie im Alltag auch, kannst du nur gleiche Dinge zusammenfassen. Aus drei Äpfeln und zwei Äpfeln kannst du logischerweise fünf Äpfel machen. Steht auf deinem Einkaufszettel aber, dass du drei Äpfel und acht Birnen mitbringen sollst, kannst du nicht nur 11 Obst draufschreiben. 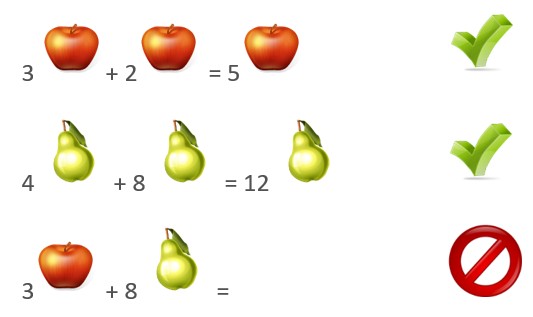 Man darf also nur gleiche Dinge addieren oder subtrahieren. Hat man aber Ausdrücke wie x², xy, x²y, xy² vor sich, dann stellt sich die Frage, welche man denn hier zusammenfassen darf. Seien x, y und z beispielsweise unterschiedliche Längen, dann handelt es sich bei x² oder x·y um eine Fläche (Länge mal Breite) und bei x³, x²y oder xyz um ein Volumen (Länge mal Breite mal Höhe). Es ist klar, dass man keine Fläche mit einem Volumen zusammenfassen kann, also lassen sich x² und x³ natürlich nicht zusammenfassen. Auch wenn es sich bei x²y und xy² beidesmal um ein Volumen handelt, so handelt es sich doch um unterschiedliche Formen und können auch nicht zusammengefasst werden. Bei xy und yx hingegen handelt es sich um dieselbe Fläche. Das fällt sofort auf, wenn wir nach dem Kommutativgesetz die Faktoren in alphabetischer Reihenfolge aufschreiben. Dann ist: xy + yx = xy + xy = 2xy 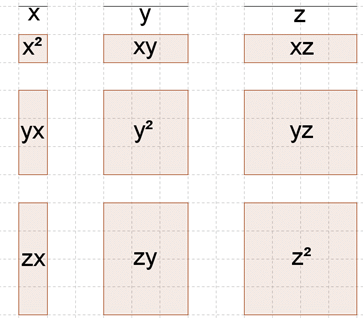 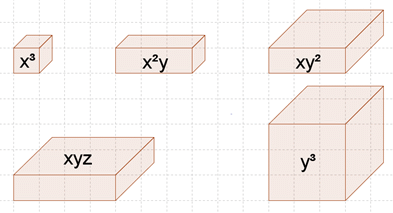 Diese Betrachtungen führen zur folgenden Regel: |
| Summanden zusammenfassen Man darf Summanden zusammenfassen, bei denen gleiche Variablen in den gleichen Potenzen vorkommen. Beispiele: 2x + 3x = 5x 3x² + 4x² = 7x² |
Zusammenfassend gilt
für das Vereinfachen von Summen:  |
| Klammerregeln bei Addition und Subtraktion |
| Werden innerhalb eines
Termes Klammern addiert oder
subtrahiert, so kann es sinnvoll sein, den Term ohne Klammern zu
schreiben. Bei der Addition ist das schon mal kein Problem. Befindet sich ein + vor der Klammer, dann darf man die Klammern in diesem Fall einfach weg lassen. 3 + (x + 4) = 3 + x + 4 Bei der Subtraktion darf man das nicht so einfach. Befindet sich ein - vor der Klammer und man will die Klammer weglassen, so muss man alle Plus- und Minuszeichen in der Klammer umdrehen. Aus Plus wird Minus und aus Minus wird Plus. 3 - (x + 4) = 3 - x - 4 Die vier Fälle, die auftreten können, finden sich in den folgenden Klammerregeln: |
| Klammerregeln bei Addition
und Subtraktion a + (b + c) = a + b + c a + (b - c) = a + b - c a - (b + c) = a - b - c a - (b - c) = a - b + c |
| Produkt einer Summe mit einer Zahl |
| Das Produkt einer Summe
mit einer Zahl lässt sich anschaulich an einem Kinobesuch in
Kaiserslautern zeigen. Gehen wir davon aus, dass 4 Freunde einen gemütlichen Kinobesuch planen. Sie gehen ins Central Kino in der City und kaufen an der Kasse viermal das Kombipaket aus Ticket und Popcorn. Beim nächsten Kinobesuch entscheiden sie sich für das UCI am Stadtrand. Dort sind die Kassen für den Eintritt und die Verpflegung getrennt. Also kaufen die 4 Freunde am Eingang erst viermal ein Ticket, um anschließend im oberen Stockwerk vier Popcorn-Tüten zu kaufen. Natürlich ist es klar, dass beide Kinobesuche gleich viel Geld gekostet haben und so haben wir eine schöne Gleichung, die uns den Sachverhalt veranschaulicht.  Jetzt mathematisieren wir diesen Zusammenhang und schreiben: 4 ·
(Ticket + Popcorn) = 4 ·
Ticket + 4 ·
Popcorn
Ist eigentlich klar. Trotzdem vergessen Schüler oft, dass auch der zweite Summand in der Klammer mit dem Vorfaktor (hier der 4) multipliziert werden muss. Vergisst man das im Kino, so würde das dazu führen, dass die vier Freunde nur eine Popcorntüte haben und es Streit gibt. Vergisst man es in der Mathearbeit, dann führt es dazu, dass man Punkte abgezogen bekommt. Man kann sich das Rechengesetz aber auch an dem folgenden Hasenkäfig veranschaulichen. Unser Hase soll einen Käfig bekommen. Die Länge des Käfigs ist die Strecke b + c, die Breite a. Der Flächeninhalt seines Käfigs beträgt somit a · (b+c). 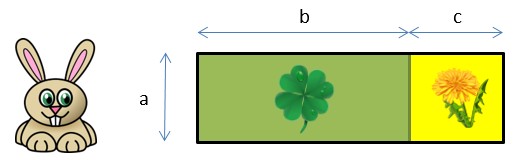 Unser Hase ist aber sehr anspruchsvoll und hätte gerne einen Teil mit Klee und einen Teil mit Löwenzahn bepflanzt. Betrachten wir die beiden Flächen, die zusammen natürlich die gesamte Käfigfläche ergeben: Die Fläche Klee entspricht a · b, die Fläche Löwenzahn a · c. 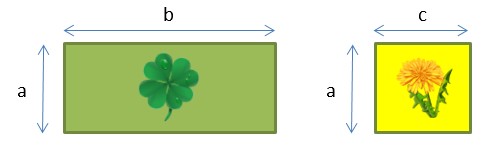 Es gilt: Gesamtfläche = Fläche Klee + Fläche Löwenzahn a · (b + c) = a · b + a · c Und schon steht das Distributivgesetz da. |
| Distributivgesetz a · (b + c) = a · b + a · c a · (b - c) = a · b - a · c Beispiel: 3 · (x + 2) = 3 · x + 3 · 2 = 3x + 6 a · (a - 3) = a · a - a · 3 = a² - 3a |
| Produkt einer Summe mit einer Summe |
|
Das
Multiplizieren einer Summe mit einer Summe lässt sich erneut
am
Hasenkäfig zeigen. Jetzt aber ist der Hase noch
wählerischer
und gibt sich mit nur zwei verschiedenen Futterpflanzen nicht mehr
zufrieden.
Die Gesamtfläche, die dem Hasen zur Verfügung steht, berechnet sich aus Länge · Breite. Somit entspricht die Fläche dem Term (a+b) · (c+d).
Die
Fläche entspricht aber auch den Einzelflächen, von
denen es
hier vier Stück gibt.
Durch Gleichsetzen der beiden Flächen erhält man: Gesamtfläche
= Fläche Klee + Fläche Löwenzahn +
Fläche Tulpen +
Fläche Veilchen (a + b) · (c + d) = a · c + a · d + b · c + b · d Für die einzelnen Summanden nimmst man den ersten Wert der ersten Klammer mit dem ersten Wert der zweiten Klammer mal, dann ersten mit zweitem, dann zweitem mit erstem und schließlich zweitem mit zweitem. Das nennt man Ausmultiplizieren. Das funktioniert auch wenn in einer oder beiden Klammern ein Minus steht. Dann müssen aber die Vorzeichen bei der Multiplikation berücksichtigt werden.
|
| Multiplikation
von Summen mit Summen (a + b) · (c + d) = a · c + a · d + b · c + b · d Bei Minuszeichen in den Klammern unbedingt die Vorzeichen beachten: (a + b) · (c - d) = a · c - a · d + b · c - b · d (a - b) · (c + d) = a · c + a · d - b · c - b · d (a - b) · (c - d) = a · c - a · d - b · c + b · d Beispiele: (3 + x) · (2 + y) = 3·2 + 3·y + x·2 + x·y = 6 + 3y + 2x + xy (2 + x) · (x - 5) = 2·x - 2·5 + x·x - x·5 = 2x -10 + x² - 5x = x² -3x -10 |
| Die binomischen Formeln |
| Die binomischen Formeln
sind ein Sonderfall der Multiplikation von Summen mit Summen. Statt (a +
b) · (c + d) stehen in beiden Klammern aber jetzt dieselben
Variablen, also (a
+
b) · (a + b). Die Umformung ist also nichts Neues: (a
+
b)² = (a +
b) · (a + b) = a² + ab + ba + b² =
a² + 2ab + b²
(a - b)² = (a - b) · (a - b) = a² - ab - ba + b² = a² - 2ab + b² (a + b) · (a - b) = a² - ab + ba - b² = a² - b² Natürlich kannst du dir das Ergebnis jedesmal wieder herleiten, wenn du die Multiplikation von Summen mit Summen beherrschst. Aber du kannst auch die Umformungsschritte zwischendrin weglassen und einfach den Rest als Binomische Formeln auswendig lernen. Für die erste binomische Formel erkennt man hier nochmal die vier Terme: a², ab, ab und b² 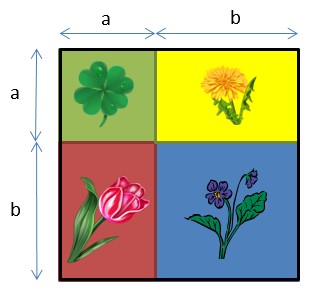 So. Jetzt einfach auswendig lernen: |
| Die
binomischen Formeln (a + b)² = a² + 2ab + b² (a - b)² = a² - 2ab + b² (a + b) · (a - b) = a² - b² Beispiele: (x + 3)² = x² + 3·x·2 + 3² = x² + 6x + 9 (5 - a)² = 5² - 2·5·a + a² = 25 - 10a + a² (3 + x) (3 - x) = 3² - x² = 9 - x² (2x + 4)² = (2x)² + 2·(2x)·4 + 4² = 4x² + 16x + 16 |
Die binomischen Formeln Nimmst
du a + b hoch 2, a
– b auch zum Quadrat, Und
dann gibt’s noch ´nen dritten Term, |
|
|
|
