
| Mathe | Physik | Informatik | Lehrer | Kontakt |
| Klassenstufe 11 - Differentialrechnung | |||||||||
| Wiederholung: Funktionswerte | |||||||||
| Betrachten wir den
Funktionsgraph einer Ortskurve. Der folgende Graph zur Funktion f(x) =
5x² soll beispielweise die Ortskurve eines Wanderers darstellen. Man kann in blau ablesen, dass er nach einer Stunde (x=1) eine Strecke von 5 km (y=5) zurückgelegt hat. Umgekehrt kann man in rot sehen, dass er zum Beispiel die Strecke von 1,8 km (y=1,8) in ungefähr 0,6 Stunden (x=0,6) zurückgelegt hat. 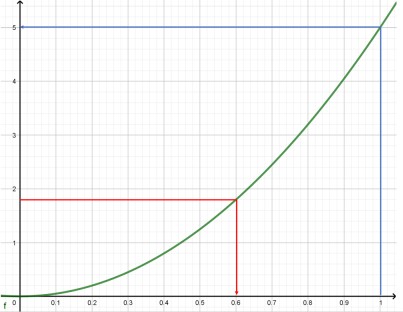 Im
folgenden interessieren wir uns aber nicht mehr für den Ort des
Wanderers, sondern für dessen Geschwindigkeit.
|
|||||||||
| Mittlere Änderungsrate | |||||||||
| Betrachtet man das
Weg-Zeit-Diagramm eines Schülers auf dem Schulweg, so kann man aus
dem Graphen sehr viel herauslesen: Wann ist er gerannt? Wann ist er gegangen? Wann ist er nochmal umgekehrt? Wann hat er Pause gemacht? 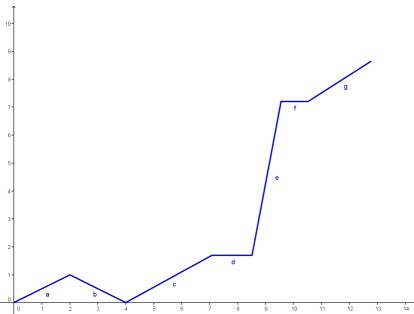 In den Abschnitten d und f hat er gewartet. Das erkennt man daran, dass die Steigung des Graphen hier 0 ist, der Graph also waagrecht verläuft. Im Abschnitt b ist er nochmal nach Hause zurück gegangen (wahrscheinlich hatte er seine Mathesachen vergessen). Man erkennt es daran, dass die Steigung hier negativ ist. Im Abschnitt b ist er gerannt. Die Steigung ist nämlich deutlich größer als beispielsweise in den Abschnitten a, c oder g. Zum Berechnen der Steigung einer linearen Funktion benötigt man zwei Punkte des Graphen: P1 (x1|y1) und P2 (x2|y2) 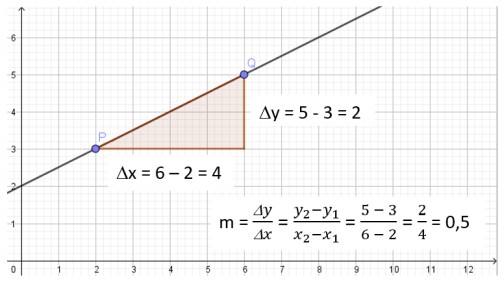 Wir veranschaulichen uns das Problem durch Einzeichnen eines Steigungsdreiecks beliebiger Größe. Es gilt für die Steigung m:  Betrachtet man jetzt keine Geraden mehr, sondern beispielsweise eine quadratische Funktion, so ist eine Aussage über die Steigung nicht mehr ganz so einfach. Anders als bei einer Geraden, die überall gleichmäßig ansteigt oder abfällt, ändert sich die Steigung einer Kurve offenbar von Punkt zu Punkt. Man muss daher zwei Geschwindigkeiten unterscheiden. Da ist zum einen die Durchschnittsgeschwindigkeit, die zum Beispiel 60km/h beträgt, wenn ich den 30km entfernten Ort in einer halben Stunde erreicht habe. Diese sagt aber nichts über die Momentangeschwindigkeit aus. Natürlich kann man auch bei einer Durchschnittsgeschwindigkeit von 60km/h mit 100km/h geblitzt werden. Die Mathematiker benutzen andere Begrifflichkeiten und reden von einer Änderungsrate. In der folgenden Tabelle ist die Übersetzung zwischen Physik und Mathematik dargestellt.
Die Berechnung der mittleren Änderungsrate erfolgt, wie man es von früher kennt, mit Hilfe des Steigungsdreiecks. Einzig spricht man jetzt nicht mehr von den Punkten P1 und P2 mit den Koordinaten (x|y), sondern von einer Stelle x0 und einer weiteren Stelle, die um ein kleines Stückchen (nennen wir es "h") weiter rechts liegt, also: x0+h. Für die y-Koordinate schreibt man f(x0) bzw. f(x0+h). Als Formel für die Berechnung der Steigung spricht man nun vom Differenzenquotienten. 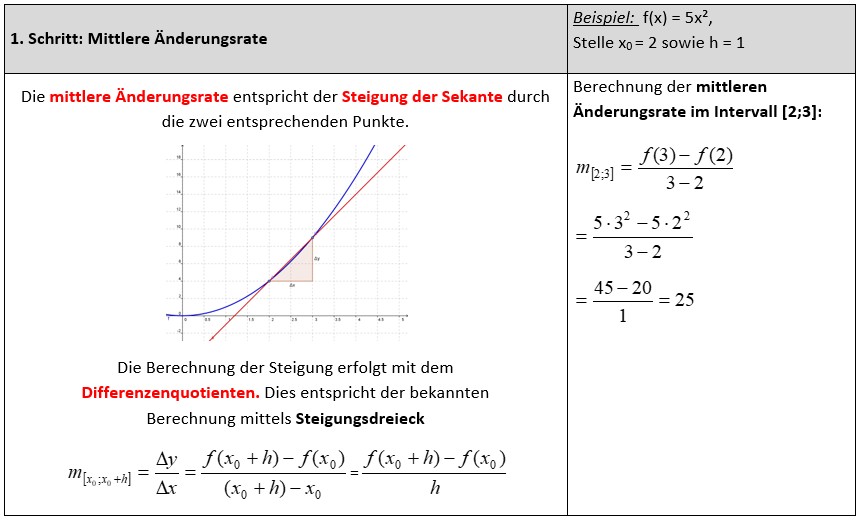 |
|||||||||
 |
 |
 |